




| GEATbx: | Main page Tutorial Algorithms M-functions Parameter/Options Example functions www.geatbx.com |
2.1 De Jong's function 1 |
The simplest test function is De Jong's function 1. It is also known as sphere model. It is continuos, convex and unimodal.
function definition:
![]()
f1(x)=sum(x(i)^2), i=1:n, -5.12<=x(i)<=5.12.
global minimum:
f(x)=0, x(i)=0, i=1:n.
This function is implemented in objfun1.
Fig. 2-1: Visualization of De Jong's function 1 using different domains of the variables; however, both graphics look similar, just the scaling changed; left: surf plot of the function in a very large area from -500 to 500 for each of both variables, right: the function at a smaller area from -10 to 10
2.2 Axis parallel hyper-ellipsoid function |
The axis parallel hyper-ellipsoid is similar to De Jong's function 1. It is also known as the weighted sphere model. Again, it is continuos, convex and unimodal.
function definition:
![]()
f1a(x)=sum(i·x(i)^2), i=1:n, -5.12<=x(i)<=5.12.
global minimum:
f(x)=0; x(i)= 0, i=1:n.
This function is implemented in objfun1a.
Fig. 2-2: Visualization of Axis parallel hyper-ellipsoid function; surf/mesh plot of the function in an area from -5 to 5
2.3 Rotated hyper-ellipsoid function |
An extension of the axis parallel hyper-ellipsoid is Schwefel's function1.2. With respect to the coordinate axes, this function produces rotated hyper-ellipsoids. It is continuos, convex and unimodal.
function definition:
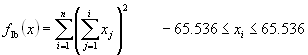
f1b(x)=sum(sum(x(j)^2), j=1:i), i=1:n, -65.536<=x(i)<=65.536.
global minimum:
f(x)=0; x(i)=0, i=1:n.
This function is implemented in objfun1b.
Fig. 2-3: Visualization of Rotated hyper-ellipsoid function; surf/mesh plot of the first two variables in an area from -50 to 50
2.4 Moved axis parallel hyper-ellipsoid function |
This function is derived from the axis parallel hyper-ellipsoid. There is a slight difference between these two function definitions. In the end the moved axis parallel hyper-ellipsoid function is more elliptic than the original function and the minimum of the function is not at x(i) = 0.
function definition:
![]()
f1c(x)=sum(5*i·x(i)^2), i=1:n, -5.12<=x(i)<=5.12.
global minimum:
f(x)=0; x(i)= 5*i, i=1:n.
This function is implemented in objfun1c.
Fig. 2-4: Visualization of Moved axis parallel hyper-ellipsoid function; surf/mesh plot of the of the first and fourth variable, the objective values were calculated from the 4-dimensional function with second and third variable set to 0
2.5 Rosenbrock's valley (De Jong's function 2) |
Rosenbrock's valley is a classic optimization problem, also known as Banana function. The global optimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial, however convergence to the global optimum is difficult and hence this problem has been repeatedly used in assess the performance of optimization algorithms.
function definition:
![]()
f2(x)=sum(100·(x(i+1)-x(i)^2)^2+(1-x(i))^2) i=1:n-1; -2.048<=x(i)<=2.048.
global minimum:
f(x)=0; x(i)=1, i=1:n.
This function is implemented in objfun2.
Fig. 2-5: Visualization of Rosenbrock's function; left: full definition range of the function, right: focus around the area of the global optimum at [1, 1]
2.6 Rastrigin's function 6 |
Rastrigin's function is based on function 1 with the addition of cosine modulation to produce many local minima. Thus, the test function is highly multimodal. However, the location of the minima are regularly distributed.
function definition:
![]()
f6(x)=10·n+sum(x(i)^2-10·cos(2·pi·x(i))), i=1:n; -5.12<=x(i)<=5.12.
global minimum:
f(x)=0; x(i)=0, i=1:n.
This function is implemented in objfun6.
Fig. 2-6: Visualization of Rastrigin's function; left: surf plot in an area from -5 to 5, right: focus around the area of the global optimum at [0, 0] in an area from -1 to 1
2.7 Schwefel's function 7 |
Schwefel's function [Sch81] is deceptive in that the global minimum is geometrically distant, over the parameter space, from the next best local minima. Therefore, the search algorithms are potentially prone to convergence in the wrong direction.
function definition:
![]()
f7(x)=sum(-x(i)·sin(sqrt(abs(x(i))))), i=1:n; -500<=x(i)<=500.
global minimum:
f(x)=-n·418.9829; x(i)=420.9687, i=1:n.
This function is implemented in objfun7.
Fig. 2-7: Visualization of Schwefel's function; surf plot in an area from -500 to 500
2.8 Griewangk's function 8 |
Griewangk's function is similar to Rastrigin's function. It has many widespread local minima. However, the location of the minima are regularly distributed.
function definition:
![]()
f8(x)=sum(x(i)^2/4000)-prod(cos(x(i)/sqrt(i)))+1, i=1:n -600<=x(i)<= 600.
global minimum:
f(x)=0; x(i)=0, i=1:n.
This function is implemented in objfun8.
The graphics in Figure 2-8 below depict Griewangk's function using three different resolutions. Each of the graphics represents different properties of the function. The graphic on the top left side shows the full definition range of the function. Here, the function looks very similar to De'Jong's function 1. When approaching the inner area, the function looks different. Many small peaks and valleys are visible in the right graphic. When zooming in on the area of the optimum, grahic on the bottom left side, the peaks and valleys look smooth.
Fig. 2-8: Visualization of Griewangk's function; top left: full definition area from -500 to 500, right: inner area of the function from -50 to 50, bottom left: area from -8 to 8 around the optimum at [0, 0]
2.9 Sum of different power function 9 |
The sum of different powers is a commonly used unimodal test function.
function definition:
![]()
f9(x)=sum(abs(x(i))^(i+1)), i=1:n; -1<=x(i)<=1.
global minimum:
f(x)=0; x(i)=0, i=1:n.
This function is implemented in objfun9.
Fig. 2-9: Visualization of Sum of different power function; surf plot in an area from -1 to 1
2.10 Ackley's Path function 10 |
Ackley's Path [Ack87] is a widely used multimodal test function.
function definition:
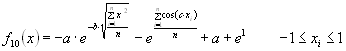
f10(x)=-a·exp(-b·sqrt(1/n·sum(x(i)^2)))-exp(1/n·sum(cos(c·x(i))))+a+exp(1) a=20; b=0.2; c=2·pi; i=1:n; -32.768<=x(i)<=32.768.
global minimum:
f(x)=0; x(i)=0, i=1:n.
This function is implemented in objfun10.
Figure 2-10 shows the function at two different zoom ratios. The graphic on the left side employs the whole definition area of the function from -30 to 30. The graphic on the right side zooms into the area of the global minimum giving a better impression of the properties of the function.
Fig. 2-10: Visualization of Ackley's Path function; left: surf plot in an area from -30 to 30, right: focus around the area of the global optimum at [0, 0] in an area from -2 to 2
2.11 Langermann's function 11 |
The Langermann function is a multimodal test function. The local minima are unevenly distributed.
function definition:
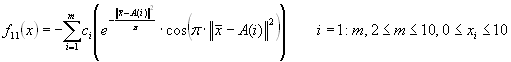
f11(x)=-sum(c(i)·(exp(-1/pi·sum((x-A(i))^2))·cos(pi·sum((x-A(i))^2)))) i=1:m, 2<=m<=10; 0<=x(i)<=10.
for the value of A and c look at the mfile objfun11.
global minimum:
f(x)=-1.4 (for m=5); x(i)=???, i=1:n.
This function is implemented in objfun11.
Figure 2-11 displays Langermann's function with different variables. The graphic on the left side shows a mesh plot of the first and second variable. The graphic on the right side uses the second and third variable while the first variable is set to 0.
Fig. 2-11: Visualization of Langermann's function; left: surf plot in an area from 0 to 10 for the first and second variable, right: same as left, but for the second and third variable
2.12 Michalewicz's function 12 |
The Michalewicz function [Mic92] is a multimodal test function (n! local optima). The parameter m defines the "steepness" of the valleys or edges. Larger m leads to more difficult search. For very large m the function behaves like a needle in the haystack (the function values for points in the space outside the narrow peaks give very little information on the location of the global optimum).
function definition:
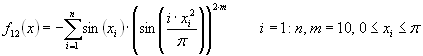
f12(x)=-sum(sin(x(i))·(sin(i·x(i)^2/pi))^(2·m)), i=1:n, m=10 0<=x(i)<=pi.
global minimum:
f(x)=-4.687 (n=5); x(i)=???, i=1:n. f(x)=-9.66 (n=10); x(i)=???, i=1:n.
This function is implemented in objfun12.
The first two graphics below represent a global and a local view to Michalewicz's function, both for the first two variables. The third graphic on the right side displays the function using the third and fourth variable, the first two variables were set to 0. By comparing the left and the right graphic the increasing difficulty of the function can be seen. As higher the dimension as more valleys are introduced into the function.
Fig. 2-12: Visualization of Michalewicz's function; top left: surf plot in an area from 0 to 3 for the first and second variable, right: area around the optimum, bottom left: same as top left for the third and fourth variable, variable 1 and 2 are set 0
2.13 Branins's rcos function |
The Branin rcos function [Bra72] is a global optimization test function. The function has 3 global optima.
function definition:
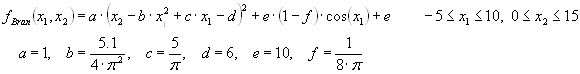
fBran(x1,x2)=a·(x2-b·x1^2+c·x1-d)^2+e·(1-f)·cos(x1)+e a=1, b=5.1/(4·pi^2), c=5/pi, d=6, e=10, f=1/(8·pi) -5<=x1<=10, 0<=x2<=15.
global minimum:
f(x1,x2)=0.397887; (x1,x2)=(-pi,12.275), (pi,2.275), (9.42478,2.475).
This function is implemented in objbran.
Fig. 2-13: Visualization of Branins's rcos function; surf plot of the definition range
2.14 Easom's function |
The Easom function [Eas90] is a unimodal test function, where the global minimum has a small area relative to the search space. The function was inverted for minimization.
function definition:
![]()
fEaso(x1,x2)=-cos(x1)·cos(x2)·exp(-((x1-pi)^2+(x2-pi)^2)) -100<=x(i)<=100, i=1:2.
global minimum:
f(x1,x2)=-1; (x1,x2)=(pi,pi).
This function is implemented in objeaso.
Fig. 2-14: Visualization of Easom's function; left: surf plot of a large area around the optimum the definition range, right: the direct area around the optimum
2.15 Goldstein-Price's function |
The Goldstein-Price function [GP71] is a global optimization test function.
function definition:
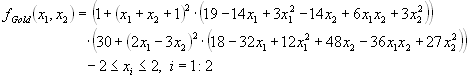
fGold(x1,x2)=[1+(x1+x2+1)^2·(19-14·x1+3·x1^2-14·x2+6·x1·x2+3·x2^2)]·
[30+(2·x1-3·x2)^2·(18-32·x1+12·x1^2+48·x2-36·x1·x2+27·x2^2)]
-2<=x(i)<=2, i=1:2.
global minimum:
f(x1,x2)=3; (x1,x2)=(0,-1).
This function is implemented in objgold.
Fig. 2-15: Visualization of Goldstein-Price's function; surf plot of the definition range
2.16 Six-hump camel back function |
The 2-D Six-hump camel back function [DS78] is a global optimization test function. Within the bounded region are six local minima, two of them are global minima.
function definition:
![]()
fSixh(x1,x2)=(4-2.1·x1^2+x1^4/3)·x1^2+x1·x2+(-4+4·x2^2)·x2^2 -3<=x1<=3, -2<=x2<=2.
global minimum:
f(x1,x2)=-1.0316; (x1,x2)=(-0.0898,0.7126), (0.0898,-0.7126).
This function is implemented in objsixh.
Fig. 2-16: Visualization of Six-hump camel back function; left: surf plot of the area surrounding the minima, right: smaller area around the minima
| GEATbx: | Main page Tutorial Algorithms M-functions Parameter/Options Example functions www.geatbx.com |